Specialist Course FS23:
Black Holes and Quantum Fields
Prerequisites, Timetable, Outline, Literature, and more ...
Updates / Latest News
- 15.05.23: Suggested Homework Problems for next week:
- Killing Vectors and Conserved Charges for Particle in a Gravitational + Maxwell Field
(section 9.4)
- Horizon Area Variation Formula and Smarr Relation for the Reissner-Nordstrom Black Hole
(sections 9.5 and 9.6)
- 14.05.23: Added Information about the Requirements for obtaining the Credits for this Course
- 14.05.23: Various Additions and Updates to the Lecture Notes (mainly section 9)
- 08.05.23: Note: last lecture Monday 22.05 (29.05 is a public holiday)
- 07.05.23: Various Additions and Updates to the Lecture Notes (mainly section 9)
- 16.04.23: Various Additions and Updates to the Lecture Notes (mainly section 8)
- 02.04.23: Various Additions and Updates to the Lecture Notes (sections 6, 7 and 8)
- 25.03.23: Various Additions and Updates to the Lecture Notes (sections 4 and 8, Appendix B etc.)
- 20.03.23: Homework for 27.03.23: Section 5.7 (Fun with Bogoliubov)
- 13.03.23: Homework for 20.03.23: Appendix A.3 (Proofs) and Appendix A.6
- 03.03.23: Added reference on QFT in Curved Spacetime:
Algebraic Approach to this Webpage
- 27.02.23: Homework for next weeek (06.03.23):
- Surface Gravity: verify calculations in section 2.6
- Derivation of the Scalar Effective Potential in section 2.9
- 26.02.23: Update to the lecture notes in sections 1 and 2
- 20.02.23: Note new schedule: Monday 15:15 -- 18:00 (in practice until approximately 17:30,
with one break; no course on Tuesday)
Summary and Overview
Much of the current and ongoing work on Quantum Gravity is motivated by
the puzzles raised by the mysterious and suprising thermodynamic properties exhibited
by Black Holes at the semi-classical level. The key observations here,
regarding both classical and semi-classical General Relativity,
go back to the 1970s. It is impossible to appreciate, let alone
understand or judge, current activities and efforts in this field
without a knowledge of these developments and discoveries
from over 40 years ago.
Nevertheless, in spite of the importance of these discoveries, and in
spite of the fact that they have had as much an impact on theoretical
gravitational physics as the more or less simultaneous development of
the Standard Model of Particle Physics has had on theoretical particle
physics, they do not appear to be part of the standard
theoretical physicists' curriculum today.
The primary aim of this course will be to (partially) fill this gap! As a consequence,
the target audience for this course are not just Master students, but
basically anybody in theoretical physics who would like to have a better understanding
of these matters.
Starting from and building on the
properties of the Rindler metric (Minkowski space
in accelerated coordinates) and the Schwarzschild Black Hole metric,
which I will review (but will assume some familiarity with), I want to
deal with the following topics:
- Classsical Theory of Black Holes
(Penrose Diagrams, uniqueness (no hair) theorems, definitions and properties of
Black Hole Horizons, and the
Laws of Black Hole Mechanics).
The treatment here will necessarily be largely cursory and heuristic,
because most of these results are rigorous mathematical theorems, and
probably most of you will not be interested in the details of these.
However, it is good (and indispensable for the following) to know the facts.
- Quantum Field Theory in Curved Spacetime
(Quantum Theory of Time-Dependent Harmonic Oscillators, Rethinking QFT in Minkowski Space,
Bogoliubov Transformations, QFT in Globally Hyperbolic Spacetimes).
- Unruh Effect
(Minkowski and Rindler Vacua, Bogoliubov Transformation between them, Unruh Temperature,
Entanglement and the Minkowski Vacuum as a Mixed Thermal State, Euclidean Perspective).
Central part of this course: detailed derivations to illustrate the general formalism, and to
simplify the subsequent discussion of Hawking temperature and radiation.
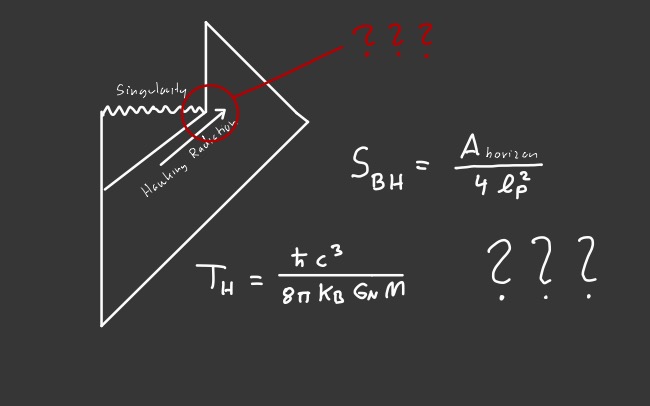
- Semi-Classical Theory of Black Holes
(Hawking Temperature, Black Hole Evaporation, Bekenstein-Hawking Black Hole
Entropy, and the Laws of Black Hole Thermodyamics).
The amount of material and
literature on this enormous, and the choice of topics and level of detail
will depend on the time available, and the energy and interests of lecturer and audience!
- Implications and Outlook
(in particular in relation to the extremely subtle (and as a consequence
much abused and misunderstood) so-called
Information Paradox and its consequences).
To a certain extent, the course will therefore (unintentionally) trace some of the
work of Stephen Hawking on these subjects. For a brief and
non-technical biographical account of his work, see
(in the course, we will deal with the subjects mentioned in sections 7, 9, 10 and 14
of this article).
Prerequisites
- Basics of General Relativity (general formalism; Rindler, Schwarzschild,
Kruskal)
- Basic Basics of Quantum Field Theory (canonical quantisation of free scalar fields,
vacuum and creation and annihilation operators) and Statistical Mechanics (better yet,
finite temperature QFT)
Schedule
- NEW: Time and Place: Monday 15:15 -- 18:00 Room 119
- Starting Date: Monday, February 20th
Tentative Outline / Preliminary List of Topics
- Introduction: Motivation and Overview
- Review of Rindler Space and the Schwarzschild Black Hole
- Carter-Penrose Conformal Diagrams
- Quantum Field Theory in Curved Spacetime
- Unruh Effect
- Hawking Temperature and Hawking Radiation
- Aspects of Black Hole Entropy and Black Hole
Thermodynamics
- Outlook/Wild Stuff: Information Paradox / Firewalls etc
Formalities / Information for Theory Master Students
Literature
- State of the Art ((Post-)Modern Black Hole Thermodynamics)
- Classical Theory of Black Holes
- My GR Lecture Notes: Lecture Notes on General Relativity (for some of the more elementary things)
- The Classic: S. Hawking, G. Ellis,
The large scale structure of space-time (for some of the earlier classical results)
- R. Wald, General Relativity
- The superb Cambridge (Part III) Lecture Notes on Black Holes (for almost everything we will cover, but done with much more expertise and detail than I will be able
to offer):
- One of my all-time favourite physics textbooks: E. Poisson,
A Relativist's Toolkit: The Mathematics of Black-Hole Mechanics
- Monographs on QFT in Curved Spacetime
- N. Birrell, P. Davies: Quantum Fields in Curved Space
- V. Mukhanov, S. Winitzki: Quantum Effects in Gravity
- L. Parker, D. Toms: Quantum Field Theory in Curved Spacetime
- R. Wald: Quantum Field Theory in Curved Spacetime and Black Hole Thermodynamics
- see also
- chapter 14 of R.M. Wald: General Relativity
- chapter 09 of S. Carroll: Spacetime and Geometry, an Introduction to General Relativity
- QFT in Curved Spacetime: Algebraic Approach
- Semi-Classical Theory of Black Holes I (Hawking Radiation)
- Semi-Classical Theory of Black Holes II (Black Hole Thermodynamics)
- Black holes and information loss paradox
- Selected Original Articles (internal UniBe access only)
Contact
- Matthias Blau, Office 220a

